
从DH算法我们可以看到,公钥-私钥组成的密钥对是非常有用的加密方式,因为公钥是可以公开的,而私钥是完全保密的,由此奠定了非对称加密的基础。
非对称加密就是加密和解密使用的不是相同的密钥:只有同一个公钥-私钥对才能正常加解密。
因此,如果小明要加密一个文件发送给小红,他应该首先向小红索取她的公钥,然后,他用小红的公钥加密,把加密文件发送给小红,此文件只能由小红的私钥解开,因为小红的私钥在她自己手里,所以,除了小红,没有任何人能解开此文件。
非对称加密的典型算法就是RSA算法,它是由Ron Rivest,Adi Shamir,Leonard Adleman这三个哥们一起发明的,所以用他们仨的姓的首字母缩写表示。
非对称加密相比对称加密的显著优点在于,对称加密需要协商密钥,而非对称加密可以安全地公开各自的公钥,在N个人之间通信的时候:使用非对称加密只需要N个密钥对,每个人只管理自己的密钥对。而使用对称加密需要则需要N*(N-1)/2个密钥,因此每个人需要管理N-1个密钥,密钥管理难度大,而且非常容易泄漏。
既然非对称加密这么好,那我们抛弃对称加密,完全使用非对称加密行不行?也不行。因为非对称加密的缺点就是运算速度非常慢,比对称加密要慢很多。
所以,在实际应用的时候,非对称加密总是和对称加密一起使用。假设小明需要给小红需要传输加密文件,他俩首先交换了各自的公钥,然后:
- 小明生成一个随机的AES口令,然后用小红的公钥通过RSA加密这个口令,并发给小红;
- 小红用自己的RSA私钥解密得到AES口令;
- 双方使用这个共享的AES口令用AES加密通信。
可见非对称加密实际上应用在第一步,即加密“AES口令”。这也是我们在浏览器中常用的HTTPS协议的做法,即浏览器和服务器先通过RSA交换AES口令,接下来双方通信实际上采用的是速度较快的AES对称加密,而不是缓慢的RSA非对称加密。
Java标准库提供了RSA算法的实现,示例代码如下:
import java.security.*;
import javax.crypto.Cipher;
import java.util.HexFormat;
public class Main {
public static void main(String[] args) throws Exception {
// 明文:
byte[] plain = "Hello, encrypt use RSA".getBytes("UTF-8");
// 创建公钥/私钥对:
Person alice = new Person("Alice");
// 用Alice的公钥加密:
byte[] pk = alice.getPublicKey();
System.out.println("public key: " + HexFormat.of().formatHex(pk));
byte[] encrypted = alice.encrypt(plain);
System.out.println("encrypted: " + HexFormat.of().formatHex(encrypted));
// 用Alice的私钥解密:
byte[] sk = alice.getPrivateKey();
System.out.println("private key: " + HexFormat.of().formatHex(sk));
byte[] decrypted = alice.decrypt(encrypted);
System.out.println(new String(decrypted, "UTF-8"));
}
}
class Person {
String name;
// 私钥:
PrivateKey sk;
// 公钥:
PublicKey pk;
public Person(String name) throws GeneralSecurityException {
this.name = name;
// 生成公钥/私钥对:
KeyPairGenerator kpGen = KeyPairGenerator.getInstance("RSA");
kpGen.initialize(1024);
KeyPair kp = kpGen.generateKeyPair();
this.sk = kp.getPrivate();
this.pk = kp.getPublic();
}
// 把私钥导出为字节
public byte[] getPrivateKey() {
return this.sk.getEncoded();
}
// 把公钥导出为字节
public byte[] getPublicKey() {
return this.pk.getEncoded();
}
// 用公钥加密:
public byte[] encrypt(byte[] message) throws GeneralSecurityException {
Cipher cipher = Cipher.getInstance("RSA");
cipher.init(Cipher.ENCRYPT_MODE, this.pk);
return cipher.doFinal(message);
}
// 用私钥解密:
public byte[] decrypt(byte[] input) throws GeneralSecurityException {
Cipher cipher = Cipher.getInstance("RSA");
cipher.init(Cipher.DECRYPT_MODE, this.sk);
return cipher.doFinal(input);
}
}
RSA的公钥和私钥都可以通过getEncoded()方法获得以byte[]表示的二进制数据,并根据需要保存到文件中。要从byte[]数组恢复公钥或私钥,可以这么写:
byte[] pkData = ...
byte[] skData = ...
KeyFactory kf = KeyFactory.getInstance("RSA");
// 恢复公钥:
X509EncodedKeySpec pkSpec = new X509EncodedKeySpec(pkData);
PublicKey pk = kf.generatePublic(pkSpec);
// 恢复私钥:
PKCS8EncodedKeySpec skSpec = new PKCS8EncodedKeySpec(skData);
PrivateKey sk = kf.generatePrivate(skSpec);
以RSA算法为例,它的密钥有256/512/1024/2048/4096等不同的长度。长度越长,密码强度越大,当然计算速度也越慢。
如果修改待加密的byte[]数据的大小,可以发现,使用512bit的RSA加密时,明文长度不能超过53字节,使用1024bit的RSA加密时,明文长度不能超过117字节,这也是为什么使用RSA的时候,总是配合AES一起使用,即用AES加密任意长度的明文,用RSA加密AES口令。
此外,只使用非对称加密算法不能防止中间人攻击。
RSA加密具体算法
RSA 非对称加密算法是一种公钥加密技术,由 Ron Rivest、Adi Shamir 和 Leonard Adleman 在1977年提出。它基于大整数分解的困难性。以下是 RSA 加密算法的基本步骤:
密钥生成
- 选择两个大素数 p 和 q:
- 这两个素数需要足够大(通常是几百位到上千位),以确保安全性。
- 计算 n = p * q:
- n 是公钥和私钥的一部分,通常被称为模数。
- 计算 φ(n) = (p-1) * (q-1):
- φ(n) 是欧拉函数,用于确定与 n 互质的整数个数。
- 选择一个整数 e:
- e 是公钥的一部分,需要满足 1 < e < φ(n),且 e 与 φ(n) 互质(即 gcd(e, φ(n)) = 1)。
- 计算 d:
- d 是私钥的一部分,是 e 关于 φ(n) 的模逆元,即 (d * e) % φ(n) = 1。
- 可以使用扩展欧几里得算法来计算 d。
公钥和私钥
- 公钥:(e, n)
- 私钥:(d, n)
加密过程
假设发送方想要加密一条消息 M(其中 M < n),加密过程如下:
- 将明文 M 转换为整数形式(如果 M 不是整数,可以先进行编码转换)。
- 计算密文 C:

解密过程
接收方使用私钥 (d, n) 来解密密文 C:
- 计算明文 M:
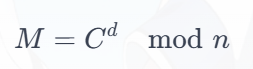
安全性基础
RSA 算法的安全性主要基于大整数分解的困难性。攻击者需要知道私钥 (d, n) 才能解密密文,而要计算私钥,必须先分解出模数 n 的两个素因子 p 和 q。对于足够大的 n,这种分解几乎是不可能在合理时间内完成的。
实际应用中的注意事项
- 密钥长度:为了保证安全性,通常建议使用至少 2048 位的密钥长度。
- 填充方案:实际应用中,通常会对明文进行填充处理(如 PKCS#1 v1.5 或 OAEP 填充),以增强安全性。
- 性能优化:RSA 加密和解密操作相对较慢,因此在实际应用中,常结合对称加密算法使用,例如通过 RSA 加密对称密钥,再用对称密钥加密数据,以提高效率。
以上就是 RSA 非对称加密算法的基本实现流程和原理。




